✅ DISEÑO CONTRA LA FILTRACIÓN EN PRESAS DE TIERRA

Uno de los principales problemas y cuidados que se deben tener presente en el diseño de las presas de tierra es la capacidad de infiltración que sucede dentro y por debajo del relleno de esta, por lo cual siempre se deberá llevar un cuidadoso control para así poder evitar y prevenir problemas con la erosión interna que permanece oculta, y a su vez, que se realiza una posible migración de materiales finos. Se debe tener en cuenta que variables como la gradiente hidráulica, la presión de poros y de infiltración, la velocidad de infiltración bajo y dentro de la presa deberán tener un restringido acceso solo a niveles aceptables para los materiales que se están empleando. Se debe tener en cuenta que toda filtración bajo una presa de tierra representa un peligro mucho mayor en comparación con las presas de concreto, esto debido principalmente a que las presas de tierra suelen construirse sobre un material suave.

RED DE FLUJO EN LA PRESA

La red de flujo viene a representar la solución gráfica de la ecuación de Laplace en dos dimensiones en función del potencial hidráulico. Representa la pérdida de energía que puede presentar en algún medio resistente siempre y cuando se presente un régimen permanente.

Se conoce como cuerpo homogéneo al que presenta las mismas características de conductividad hidráulica en cualquier punto de toda su sección, además si la conductividad hidráulica también es la misma en todas sus direcciones, se contará con un medio isótropo, presenta la presa un material homogéneo e isótropo. En cambio, si la conductividad hidráulica es cambiante en cualquier dirección, se dirá que la presa es de material homogéneo y anisótropo, lo cual se debe principalmente al grado de compactación que presenten las presas, ocasionando que la conductividad en el eje horizontal sea mayor que la conductividad el eje vertical. Una de las características principales de un medio homogéneo e isótropo es que el conjunto de las líneas de corriente con el conjunto de las líneas equipotenciales, construirán una malla ortogonal que también se la conoce como red de flujo, a diferencia en un medio anisótropo, en el cual la dirección del conjunto de líneas de corriente no tendrá concordancia con el conjunto de líneas equipotenciales.

Se dice que un medio es heterogéneo y anisótropo cuando este presenta características de conductividad hidráulica variable en cada uno de sus puntos y sus direcciones. Una presa es heterogénea cuando esta presenta de dos a más zonas homogéneas y anisótropas.

LINEA DE FILTRACIÓN SUPERIOR EN MATERIAL HOMOGÉNEO E ISÓTROPO

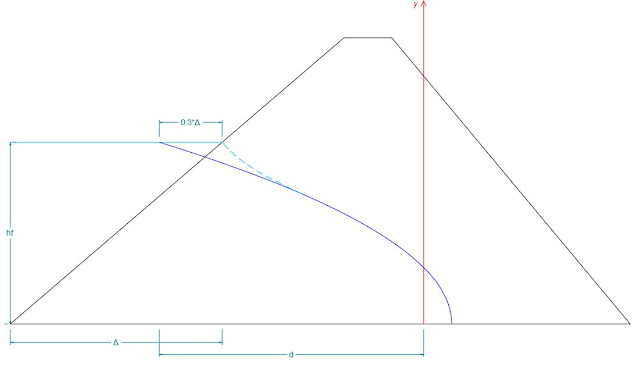
La forma y posición de la línea de filtración superior (LFS) se requiere principalmente para poder obtener la red de flujo en la sección de la presa, esta atraviesa la cortina según sea la geometría propuesta, y, además, es necesario conocer las características de permeabilidad y granulometría de los materiales de la presa. Uno de las principales metodologías para la obtención de la LFS es la de Kozeny, quien estudio la filtración a través de una cortina homogénea y presentando una cara aguas arriba parabólica la cual descansa sobre la superficie impermeable y el dren horizontal de material permeable. Estas superficies presentan un ángulo de 180° grados entre sí, además tiene un origen de coordenadas en el punto inicial de dren bajo la presa.

La parábola que graficó Kozeny sigue la expresión:

Además, el ingreso al dren siempre lo hará con un ángulo perpendicular. Según Casa Grande, esta parábola trazada debe corregirse de tal manera que presente una línea de ingreso desde el NAMO en forma perpendicular con el talud de la cortina aguas arriba.

El dren de la presa puede ser de distintas formas, ocasionando que el ángulo que se forma entre la superficie permeable e impermeable sea menor que 180°. Cuando se presente esta condición, Casagrande propone modificar la línea de filtración superior en función de los valores encontrados luego de su estudio.

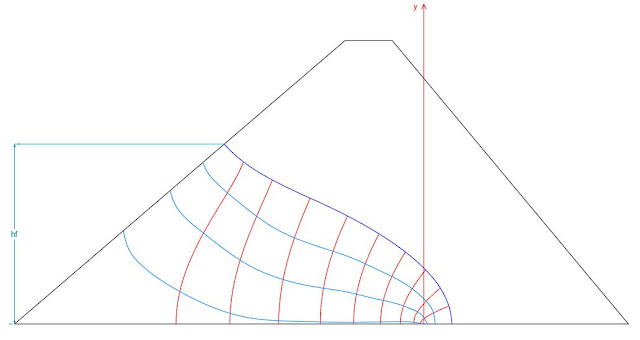
RED DE FLUJO EN UNA CORTINA HOMOGÉNEA E ISÓTROPA

Luego de haber trazado la línea de filtración superior, se debe identificar la pérdida de carga total (hf) que sufrirá la presa, valor que puede estar representado por la altura del NAMO si se contara con un dren horizontal en el fondo. La pérdida de carga deberá dividirse en partes iguales para luego trazar líneas horizontales que cortarán a la línea de filtración superior. El talud aguas arriba de la cortina es la primera línea equipotencial que se considera, luego de esto, se irán trazando las demás líneas equipotenciales desde los puntos de corte encontrados con anterioridad, siguiendo con cuidado de hacerlo con perpendicularidad y que formen 90° con las líneas de corriente. También se debe tener en cuenta que en la zona de filtración se deben trazar tubos de corriente tratando de conseguir la forma cuadrada con las líneas equipotenciales. 

Una vez obtenida la red de flujo será posible poder estimar el caudal de filtración por unidad de ancho de cortina, siguiendo la siguiente ecuación:

Donde q será el caudal de filtración por unidad de ancho en m3/ s/ m, K es la conductividad hidráulica, Nf es la cantidad de tubos de corriente, Nd es la cantidad de líneas equipotenciales y hf es la pérdida total de carga.

A su vez, será posible estimar el gradiente hidráulico por cada elemento de la red de flujo, lo cual se hará siguiendo la ecuación:

Donde i es el gradiente hidráulico, Dh es la caída de potencial y b será el mínimo recorrido de agua en el elemento seleccionado.

Cuando se trabajo con un material anisótropo, debemos tener en cuenta que el conjunto de líneas de corriente no será ortogonal con el conjunto de líneas equipotenciales, razón por la cual se debe realizar la transformación de una sección homogénea y anisótropa a una sección homogénea e isótropa. La conductividad hidráulica en un medio anisótropo puede representarse por una elipse, cuando se realice la transformación a una sección isótropo, esto exige que la elipse se convierta en una circunferencia, esto quiere decir que, la transformación de una sección a otra, representará la reducción o cambio de escala en una sola dirección, esto dependerá si se reduce el eje mayor de la elipse o se aumenta su eje mayor.